itrochoïde
Epitrochoid, Epitrochoide

Paramétrisation complexe : , soit  où a  est le rayon du cercle de base, b = a / q  celui du cercle roulant et d = k b la distance du point au centre du cercle mobile. Paramétrisation cartésienne : .

Les épitrochoïdes sont les courbes décrites par un point lié à un cercle (C) roulant sans glisser sur un cercle de base (C₀), les disques ouverts de frontières (C) et (C₀) étant disjoints ; ce sont donc les courbes que l'on obtient avec un spirographe avec disque externe.

Voir :

http://www.fciencias.unam.mx/ensmat/matsinter/c_espir_m.html http://www.math.dartmouth.edu/~dlittle/java/SpiroGraph/

Autrement dit, ce sont aussi les roulettes d'un mouvement plan sur plan dont la base est un cercle et la roulante un cercle extérieur au premier.

Pour d = b, soit k = 1, on obtient les épicycloïdes.
Pour d = a + b, on obtient les rosaces .

Pour k < 1, la courbe s'appelle aussi épicycloïde raccourcie.
Pour k > 1, la courbe s'appelle aussi épicycloïde allongée.

Toute épitrochoïde est aussi une péritrochoïde (propriété de double génération) : cercle fixe de rayon 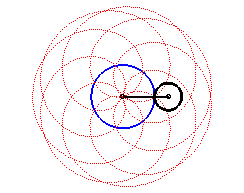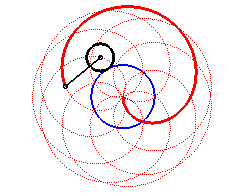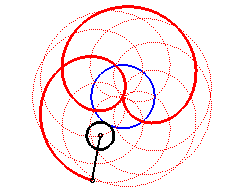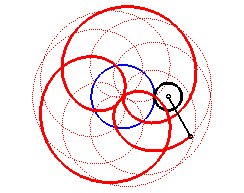, cercle mobile de rayon  et distance du point au centre du cercle mobile d' = a + b.

Pour  k = q + 1 (soit d = a + b)), on obtient une rosace avec n < 1 :.

On peut aussi définir les épitrochoïdes comme les trajectoires d’un mouvement somme de deux mouvements circulaires de mêmes sens et de vitesses angulaires distinctes, de paramétrisation complexe :  () ; ce sont des épicycloïdes si , des épicycloïdes allongées si  des épicycloïdes raccourcies si  (on peut alors prendre , , d = r₂, donc ).
Durer a baptisé ces courbes, lorsque , soit q = 1, des arachnées.

Les hypotrochoïdes et les épitrochoides constituent les trochoïdes à centre (voir aussi une généralisation sur cette page).

http://www.motorlegend.com/new/technique/rotatif/

© Robert FERRÉOL, Jacques MANDONNET 2006