Kepler's Laws and Newton's LawsM. Darby Dyar
|
|
Kepler's Laws and Newton's Laws
Kepler's LawsJohannes Kepler (1571-1630) developed a quantitative description of the motions of the planets in the solar system. The description that he produced is expressed in three ``laws''.
Kepler's First Law:The orbit of a planet about the Sun is an ellipse with the Sun at one focus.
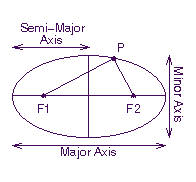
Figure 1 shows a picture of an ellipse. It is constructed by specifying two focus points, F1 and F2, of the ellipse. All points on the ellipse, such as P in Figure 1, have the property that the sum of the distance between P and F1 and the distance between P and F2 is a constant. The dimension of an ellipse is often described by giving its major axis and minor axis. In descriptions of orbits in the solar system, however, it is more common to use the semi-major axis to describe the size of the orbit, and the eccentricity of the ellipse to describe its shape. The eccentricity is given by the ratio of the distance between the two focus points to the length of the major axis of the ellipse. The periapsis, or the shortest distance between the orbiting body and the central mass, is determined by the product of the semi-major axis and the complement of the eccentriciy (1 - e): if the body is orbiting the sun, this is the perihelion, symbolized by q): q = a (1 - e). A circle is a special case of an ellipse, with an eccentricity of 0, or so that q = a.
Kepler's Second Law:A line joining a planet and the Sun sweeps out equal areas in equal intervals of time.
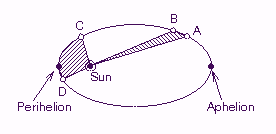
Figure 2 illustrates Kepler's Second Law. Consider the line between the Sun and point A on the elliptical orbit. After a certain amount of time, the planet will have moved along the orbit to point B, and the line between the Sun and the planet will have swept over the cross hatched area in the figure. Kepler's Second Law states that for any two positions of the planet along the orbit that are separated by the same amount of time, the area swept out in this manner will be the same. Thus, suppose that it takes the planet the same amount of time to go between positions C and D as it did for the planet to go between positions A and B. Kepler's Second Law then tells us that the second cross hatched area between C, D, and the Sun will be the same as the cross hatched area between A, B, and the Sun. Kepler's Second Law is valuable because it gives a quantitative statement about how fast the object will be moving at any point in its orbit. Note that when the planet is closest to the Sun, at perihelion, Kepler's Second Law says that it will be moving the fastest. When the planet is most distant from the Sun, at aphelion, it will be moving the slowest.
Kepler's Third Law:The squares of the sidereal periods of the planets are proportional to the cubes of their semimajor axes. We have defined the semimajor axis of the orbit above, in our discussion of Kepler's First Law. The sidereal period of a planet's orbit is the time that it takes a planet to complete one orbit around the Sun. Kepler discovered a quantitative relationship between these two properties of the orbit. If P is the period of the orbit, measured in years, and a is the semimajor axis of the orbit, measured in Astronomical Units, then P2 = a3
Newton's LawsKepler's Laws are wonderful as a description of the motions of the planets. However, they provide no explanation of why the planets move in this way. Moreover, Kepler's Third Law only works for planets around the Sun and does not apply to the Moon's orbit around the Earth or the moons of Jupiter. Isaac Newton (1642-1727) provided a more general explanation of the motions of the planets through the development of Newton's Laws of Motion and Newton's Universal Law of Gravitation.
Newton's Laws of MotionOne way to describe the motion of an object it to specify its position at different times. Consider the car in Figure 3. We can tell where it is at different times as it travels down a road. It starts at milepost 0. One minute later it is between mileposts 1 and 2 at a distance of about 1.3 miles from the start. Two minutes later, the car has gotten to a distance of about 3.3 miles from the start. In general, we could specify a unique position for the car at any time. For example, we might have written down where the car was at a time 1.5 minutes after the start, and even if we hadn't, we're pretty sure that the car was, in fact, somewhere. Mathematicians call this kind of a relationship a function. When we say that the position of the car is a function of time, it just means that there is a unique location for the car for any time. For a planetary orbit, we can describe the orbit in the same way, by providing the position of the planet along the orbit for all times.
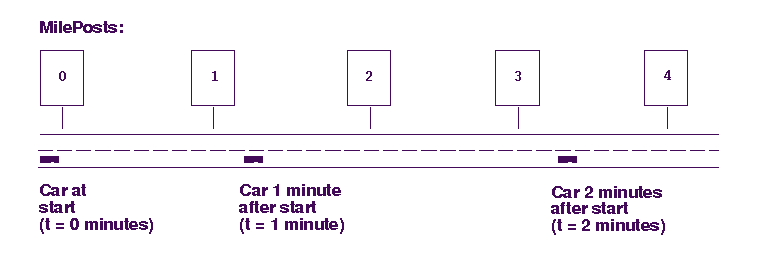
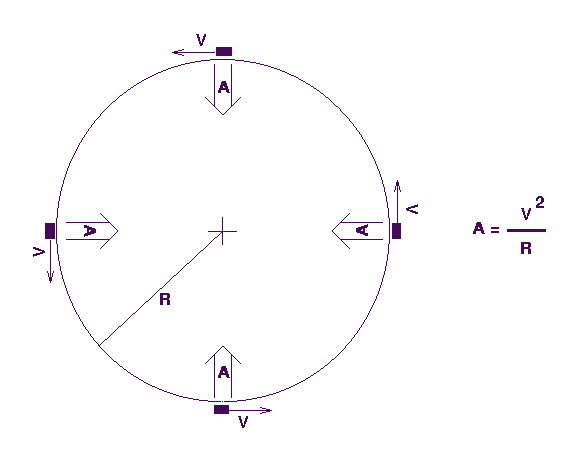
Another useful property for describing motion is the velocity of the object. Velocity is defined to be the change of position with change in time. Thus, for our car moving along the road, we can find the velocity by dividing the distance travelled by the time it takes to travel that distance. In our example, during the first minute, the car travels 1.3 miles along the road. Thus, the car's velocity would be 1.3 miles per minute (or about 78 miles per hour!) on the average during that first minute. It is important to note that physicists are very particular about the definition of velocity, and when we state a velocity we always make a statement about the direction of the motion. In our one dimensional case, this corresponds to my statement that the the car moved along the road. In general, if we were looking at a road map, we might say that the velocity was 1.3 miles per minute towards the East -- if the street ran towards the East. Velocity always is specified by both a value and a direction. A final useful property for describing motion is the acceleration of the object. Just as the velocity describes the rate of change in the position of the object, the acceleration describes the rate of change of the velocity. In our example, the car moved farther during its second minute of travel than it did during its first minute. The average velocity during the second minute would be 2 miles per minute (120 miles per hour), since the car covered two miles from 1.3 to 3.3 during the one-minute time interval from 1 minute after the start to 2 minutes after the start. The velocity increased a lot (0.7 miles per minute) between the first minute of travel and the second minute of travel, and we describe this change by the acceleration. In this case, the car's velocity increased by 0.7 miles per minute in a time interval of one minute. Thus, we'd say that the average acceleration of the car during this time was 0.7 miles per minute PER MINUTE --- acceleration is the rate of change of the velocity. Like velocity, acceleration has both a value and a direction implied. In our example, the direction was ``along the road'', but in a more general case, the acceleration is not necessarily in the same direction as the velocity. An especially good example for understanding the solar system is the case of uniform circular motion. Lets consider the case below of a car moving around a circle. The speed is constant in this motion, but the direction is changing continuously -- note the arrows showing the direction of motion in the figure -- so there must be an acceleration here. The acceleration in this special case of circular motion is called the centripetal acceleration. It is always in the direction of the center of the circle, as indicated in the figure, and it has a value, A, of A = v2 / R where v is the speed of the object along its circular path, and R is the radius of the circle.
Newton's First Law of Motion:A body remains at rest or moves in a straight line at a constant speed unless it is acted upon by an outside force. If you look back at the definition of acceleration, you will see that: (1) a body at rest is not accelerating; and (2) a body moving in a straight line at a constant speed is not accelerating either. Thus, the first law of Newton says that objects do not accelerate unless they are acted upon by an outside force.
Newton's Second Law of Motion:If a force, F, works on a body of mass M, then the acceleration, A, is given by F = M A The first law said that if there is acceleration, then there is a force. Newton's second law gives a quantitative relationship between the force and the acceleration that is observed. The relationship depends on a new property of the object, its mass. The mass is simply a measure of the amount of material in the object; mass is conventionally measured in grams or kilograms. Note that the second law implies that, for a given force, a less massive body will accelerate more than a more massive body. This is consistent with the world you are familiar with. Shove your kid brother, he might move a long way; shove Shaquille O'Neal with the same force and he won't move that far...
Newton's Third Law of Motion:If one body exerts a force on a second body, the second body exerts an equal and opposite force on the first. This law is sometimes called the ``Action-Reaction'' law. Consider what happens if you are in one row boat and you pull on a line attached to a second row boat. When you pull the line, you exert a force on the second boat. But, by the third law, the other boat exerts an equal and opposite force back on you. Thus, if the second row boat has a large shipment of bricks in it so it is very heavy, your lighter boat may do all the moving even though you are doing all the pulling.
Implications for the PlanetsThe elliptical orbits of the planets have such small eccentricities that, to a very good approximation, we can think of them as circles. (Only very precise measurements, like those available to Kepler, are able to detect the difference.) This means that we can use the idea of uniform circular motion to analyze planetary motion. In that section, we revealed that a body in uniform circular motion was constantly accelerating towards the center of its circular track. Thus, according to Newton's first law of motion, there must be a force acting on the planet that is always directed toward the center of the orbit -- that is toward the Sun! Newton's second law of motion allows us to state what the magnitude of that force must be. The required force is just the mass of the Earth times its acceleration. We know that the acceleration of an object moving in uniform circular motion is A = V2/R. Thus, we can calculate the force that is required to keep the Earth on its circular path and compare it to physical theories about what that force might be. This is what Newton later did, although he did it first for the Moon rather than the Earth, to learn about the force of Gravity. Finally, let us consider an implication of the ``action-reaction'' law. If there is a force that attracts the Earth toward the Sun, then there must be an equal and opposite force attracting the Sun towards the Earth. Why, then, doesn't the Sun move? The answer is that it does move, but by a very small amount since the mass of the Sun is about half a million times that of the Earth. Thus, when subjected to the equal and opposite force required by the third law, it accelerates about half a million times less than the Earth as well. For this reason, to a very good approximation, we can treat the Sun as stationary in our studies of planetary motion.
Newton's Universal Law of GravitationBy now you must be wondering: ``What is the Force that keeps the Earth going around the Sun?'' Newton's great discovery was the force of {\sl gravity}, which is an attractive force that occurs between two masses. The Universal Law of Gravitation is usually stated as an equation: Fgravity = G M1 M2 / r2 where Fgravity is the attractive gravitational force between two objects of mass M1 and M2 separated by a distance r. The constant G in the equation is called the Universal Constant of Gravitation. The value of G is: G = 6.67 X 10-11 meters3 kilograms-1 seconds-2 Newton's great step was developing this law and using it, with his laws of motion, to explain the motion of lots of different things --- from falling objects to planets. Amazingly, out of these simple and general rules, Newton was able to show that all of Kepler's descriptive laws for orbits followed as a direct consequence. When you combine Newton's gravitation and circular acceleration, which must balance in order for the object to remain in orbit, you get a nice relation between the period, distance, and mass of the central body. It beings by equating the centripetal force (Fcent) due to the circular motion to the gravitational force (Fgrav): Fgrav = Fcent
Fgrav = G m1 m2 / r2 Let the Earth be m1 and the Moon be m2. For circular motion the distance r is the semi-major axis a. The orbital velocity of the Moon can be described as distance/time, or circumference of the circular orbit divided by the orbital period: V = 2 pi r /P so setting the forces equal yields G m1 m2 / a2 = m2 V2 /a note that the m2 will cancel, so that circular orbital motion is independent of the mass of the orbiting body! G m1 / a2 = ((2 pi a)2/P2)/a which we rearrange to place all the a-terms on the right and all the P-terms on the left: G m1/(4 pi2) P2 = a3 which should look startlingly like Kepler's third law, but this time for the Earth's mass (or any other) instead of the sun's mass. To use a and P to solve for mass, manipulate once more so that m1 = a3 (4 pi2/G) / P2
|
|
Illustration: Darby Dyar
Source: Mount Holyoke College, AST 223/23 Planetary Science course, Darby Dyar This web site is a Jan.-Feb. 2018 accessed archive copy of the original version, saved at TYCHOS.info to preserve the web reference. External links may no longer be valid. Source URL: https://www.mtholyoke.edu/courses/mdyar/ast223/orbits/orb_lect.html According to the |